清华光学AI登Nature，物理神经网络，不需要反向传播。

用尽神经网络训练，最新登上Nature的清华成果！

反向传播算法不能应用怎么办？

它们提出了一个全前向方式（Fully Forward Mode，FFM）训练方法，在物理光学系统中直接执行训练过程，克服了传统数字计算机模拟的限制。

简而言之，物理系统必须在之前进行。详细建模，然后在电脑上模拟这些模型来训练网络。FFM方法避免了建模过程，允许系统直接使用测试数据进行学习和优化。

也就是说，训练不需要从后到前检查每一层(反向传播)，而是可以直接进行。从前到后更新网络参数值。

比如像拼图一样，反向传播需要先看最后一张照片(导出)，然后反向检查和恢复；FFM方法更像是手中已经完成的拼图，只需要按照一些光原理(对称互易)继续添加，不需要回去检查之前的拼图。

这样，使用FFM优势也很明显：

一是减少对数学模型的依赖性，能避免模型不准确造成的问题；节省了时间(同时能耗更低)光学系统可以并行计算大量数据和使用，消除反向传播也会减少整个网络中需要检查和调整的过程。

同一篇论文是清华的薛智威和周天邈，通讯作者是清华的方璐教授和戴琼海教授。此外，清华电子系徐智昊和之江实验室虞绍良也参与了这项研究。

消除反向传播

总结FFM原理的一句话：

现场神经网络将光学系统投射为参数化。，通过测量导出光场计算梯度，并使用梯度降低算法更新参数。

简而言之，就是让光学系统自学，通过观察自己如何处理光源(即测量导出光场)来了解自己的表现，然后通过这些信息逐步调整自己的设置(参数)。

下图显示了FFM在光学系统中的表现。运行机制：

其中a是传统设计方法的局限性；b是光学系统的组成；C是从光学系统到神经网络的投射。。

就进行而言，一般的光学系统（b），包括自由空间镜片光学和集成光子学，由分配区(深绿色)和传播区(浅绿色)组成。在这些区域中，分配区域的折射率是可调的，而且传播区的折光率是固定的。

而且这里的调配和传播区域可以映射到神经网络中。重量与神经元相连。

这些可调节的部分在神经网络中就像神经元的连接点，可以改变它们的强度(权重)来学习。

运用空间对称互易原理，同样的前向物理传播过程和测量方法可以与数据误差计算共享。

这个有点像镜子里的反射。，系统的每个部分都可以以同样的方式响应光的传播和错误的反馈。这意味着无论光线如何进入系统，系统都可以以一致的方式处理，并根据结果调整自己。

通过这种方式，可以直接在现场计算梯度，以更新设计区域的折射率，从而优化系统性能。

通过现场梯度下降法，在达到最佳状态之前，光学系统可以逐步调整其参数。

原文将上述全向模式的梯度降低方法(取代反向传播)用方程的最后表示为：

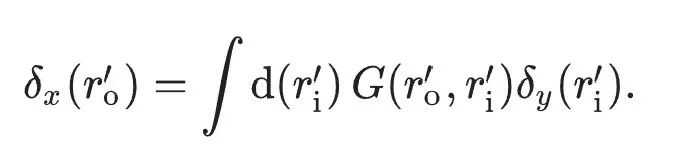
一种光学神经网络训练方法

FFM作为一种光学神经网络训练方法，具有以下优点：

准确率等于理想模型。

FFM可用于自由空间。光神经网络（Optical Neural Network，ONN）实现有效的自我训练过程。

为了解释这一结论，研究人员首先使用了一个单层的ONN在基准数据集中进行目标分类训练（a）。

具体而言，他们使用了一些手写的图片(MNIST数据)来训练这个系统，然后将结果进行可视化。（b）。

数据显示，在实验光场和理论光场之间，通过FFM学习训练的ONN非常相似(SSIM超过0.97)。

也就是说，它学得很好，几乎可以完美地复制给它的例子。

但研究人员也提醒：

因为系统存在的不完美之处，光场和梯度在理论上并不能完全准确地反映实际的物理变化。

下一步，研究人员使用更复杂的图片（Fashion-MNIST数据)训练系统识别不同的潮流对象。

起初，当层数从2层增加到8层，计算机训练网络几乎只有理论准确度才能达到平均精度。一半。

并且通过FFM学习方法，系统的网络精度提高到92.5%，接近理论值。

由此可见，传统方法训练的网络性能随着传输层数的增加而下降，而FFM学习能够保持高精度。

与此同时，通过将军非线性激活纳入FFM学习，可以进一步提高ONN的性能。实验中，非线性FFM学习可以将分类准确率从90.4%提高到93.0%。

通过进一步的研究证明非线性ONN批量训练，错误的传播过程可以简化，训练时间只增加1-1.7倍。

聚焦高分辨率的能力

FFM也可以在实际应用中实现高质量的显像，即使在复杂的透射环境中也可以实现分辨率接近物理极限。

第一，当光波进入透射介质(如雾、烟或生物组织等)时，聚焦会变得复杂，但光波在介质中的传播通常是对称的。

FFM就使用这种对称性，为了减少透射效应对焦点的负面影响，优化光波的传播路径和相位。

它的效果也非常明显，图b显示了FFM和PSO(粒子群优化)这两种优化方法的对比。

具体而言，试验使用了两种透射介质，一种是随机相位板（Scatterer-I），另外一种是透明胶带（Scatterer-II）。

这两种介质中，FFM只经过25次设计迭代。实现收敛(更快找到提升解)，收敛损失值分别为1.84和2.07(性能越小越好)。

而且需要PSO方法至少400次在最终收敛时，设计迭代可以实现收敛，损失值为2.01和2.15。

与此同时，图c显示了FFM。不断提升自己，其设计焦点逐渐从最初的随机分布演变到紧密的焦点。

在3.2 mm × 3.2 在mm的设计区域内，研究人员对FFM和PSO优化的焦点进行了进一步的对称取样，并对FWHM(半峰全宽)和PSNR(峰值信噪比)进行了对比。

数据显示，FFM聚焦精度更高，成像质量更好。

图E在扫描位于透射介质后面的分辨率图时，进一步评估了设计的焦点阵型的性能。

结果令人惊讶，FFM设计的焦点尺寸接近64.5 µm的衍射极限，这是最高分辨率的光学成像理论标准。

可将视线外的物体并行显示。

由于透射介质如此强大，研究人员再次尝试非视距（NLOS）情景，也就是说，物体隐藏在视野之外。

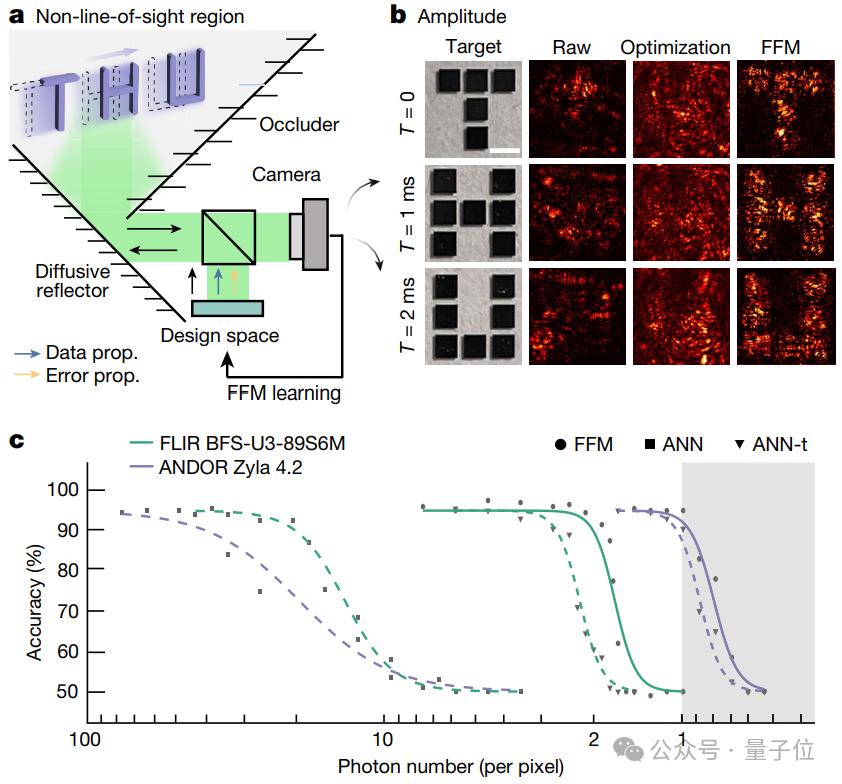
FFM利用光路空间对称从隐藏物体到观测者，允许系统通过全光学在现场重建和分析动态隐藏物体。

通过在输入波之前设计，FFM可以同时将物体中的所有网格投射到其目标位置，从而实现隐藏物体的并行恢复。

实验中使用了隐藏铬靶的字母形状。T”、“H”和“U”，并设置曝光时间(1ms)和光功率(0.20) mW），为了快速显示这些动态目标。

数据显示，图像在没有FFM设计的波之前会严重扭曲。而且FFM设计的波之前可以恢复所有三个字母的形状，SSIM(结构相似度指数)达到1.0，表明与原始图像的高度相似。

再者，神经网络算法（ANN）FFM在光子效率和分类性能方面明显优于ANN，尤其在低光子环境下，。

具体来说，FFM可以在光子数量有限的情况下(例如，许多反射或高度漫射的表面)自适应地纠正波前畸变，并且需要更少的光子来准确分类。

自动搜索非Hermitian系统中的异常点

FFM方法不仅适用于自由空间光学系统，而且可以扩展到自我设计集成光子系统。

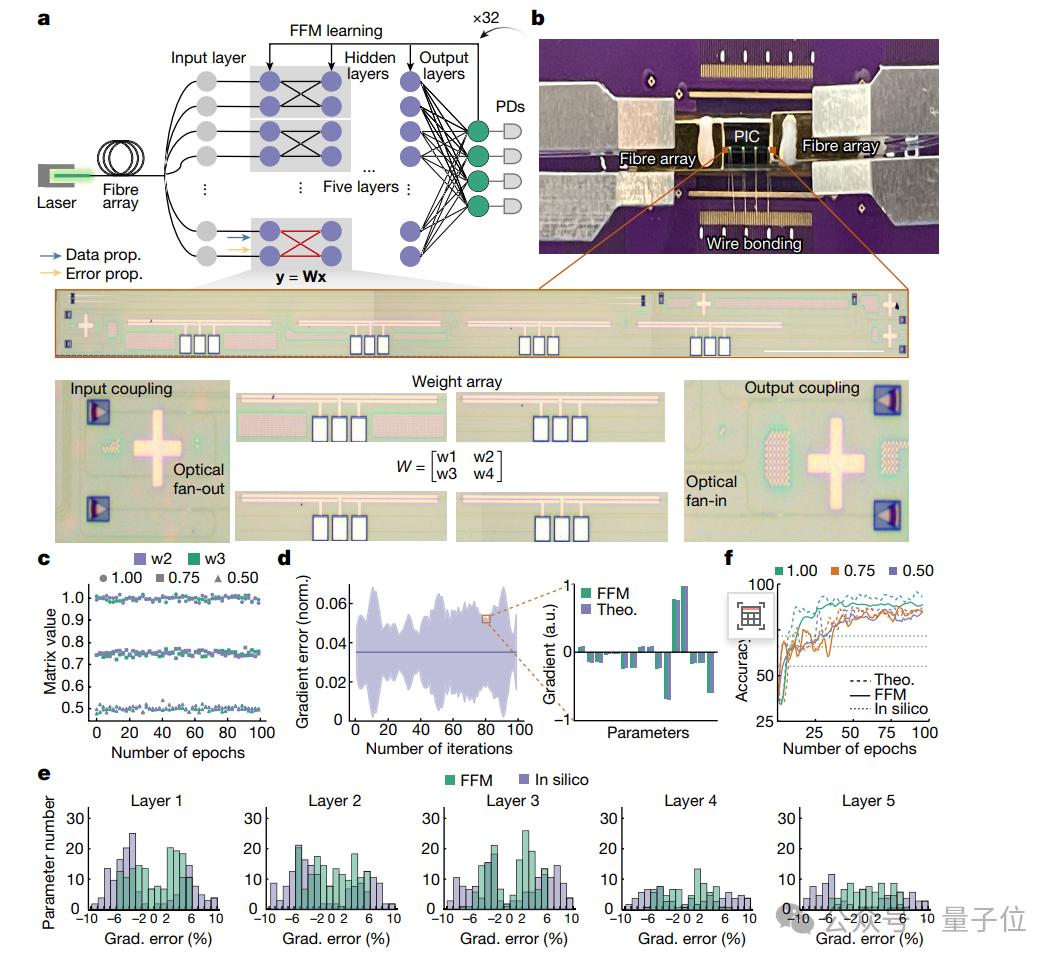
研究人员使用串联和并联设备光子核心对称，构建了一个集成神经网络（a）。

在实验中，对称核心配备了可变光衰减器，通过不同水平的注入电流。（VOA），为了模拟不同的权重，完成了不同的衰减系数。

对称核心中的编程矩阵值在图c中具有较高的保真度，时间漂移的标准偏差分别为0.012%、0.012%和0.010%，说明矩阵值很稳定。

并且，研究人员每一层的偏差都可视化。与实验梯度和理论模拟值相比，平均偏差为3.5%。

在大约100次迭代（epoch）之后，网络达到了收敛状态。

测试数据显示，在三种不同对称比例的配置下(1.0、网络分类准确率为94.7%，0.75或0.5。、89.2%和89.0%。

通过FFM获得的神经网络分类准确率为94.2%、89.2%和88.7%。

相比之下，如果使用传统的计算机模拟方法来设计网络，测试的分类精度将会更低，分别为71.7%、65.8%和55.0%。

最后，研究人员还展示了FFM的能力非厄米特系统自我设计，通过数值模拟，不需要概念模型可以实现对特定点的遍历。

非厄米特系统是物理学中的一个概念，它涉及到量子力学和光学领域的系统，这些系统不能满足厄米特性。（Hermitian）条件。

厄米特性与系统的对称性和能量实数性有关，而非厄米特系统不满足这些条件，可能会有一些特殊的物理变化，比如特异性。（Exceptional Points），在某些点上，系统的动力学行为会发生奇怪的变化。

总而言之，FFM是一种实现物理系统计算密集型训练过程的方法，能有效地并行执行大多数机器学习操作。

欢迎查阅原文，了解更多详细的测试设置、数据准备流程。

代码：https://zenodo.org/records/10820584

《Nature》原文：https://www.nature.com/articles/s41586-024-07687-4

本文来自微信微信官方账号“量子位”，作者：一水，36氪经授权发布。

本文仅代表作者观点，版权归原创者所有，如需转载请在文中注明来源及作者名字。

免责声明：本文系转载编辑文章，仅作分享之用。如分享内容、图片侵犯到您的版权或非授权发布，请及时与我们联系进行审核处理或删除，您可以发送材料至邮箱：service@tojoy.com