KAN的核心团队令人震惊。中国MIT人首次用AI发现了一个全新的物理方程。

MaxxMax科学家刚刚提出KAN。 Tegmark和北京大学同学刘子鸣，又出现了一项重磅研究！团队发现，他们用AI在物理学中找到了新的方程。从那以后，AI很可能被引入物理学研究领域，帮助人类科学家做出新的发现。

就在刚才，MIT科学家用AI发现了一个新的物理方程。

论文地址：https://arxiv.org/abs/2405.04484

作者说：本文没有解决核聚变问题，价值数百万美元，而是在更简单的设置中引入了一个有前途的概念验证。

偏微分方程（PDE），可以算是科学家的面包和黄油，但是它们极为罕见，人类科学家仅靠纸笔是很难发现的。

所以，研究人员推出了一个名为OptPDE的AI系统。

利用这一AI，可以发现新的、从未见过的可积偏微分方程！

具体而言，在使用了5000个随机初始化的PDE系数运行OptPDE之后，研究人员发现了4个可积偏微分方程，其中一个已知，另外三个是全新的方程。

MIT科学家利用这一首创的机器学习方法，为物理学提供了一种全新的研究模式。

此后，人类可以向系统提供领域知识，AI可以产生希望的假设，然后人类可以进行解释和验证。

这样就实现了整个物理发现的闭环。

01 网民：AI将颠覆每一个科学领域

网民们对这项研究表示震惊。

「太烧脑了！如果我对他们的意思有一个正确的认识，那么这个AI真的很强大很可怕！能够根据需要生成模型库模拟物理系统是一项非常巧妙的技能，可以从AI驱动的处理中节省大量的计算。」

「即使只是从这些角度来看，我们拥有的AI也可以为各个科学领域提供新的见解和想法，它将会变得更好！」

「我只是打开看看Max是不是？ Tegmark大神的研究，果然如此。」

这个网友给出了更专业的解释。——

本质上，由于偏微分方程具有较多的CQs，并且自然系统遵循定律(例如热学)，所以它们在偏微分方程中应用了奖励函数。

这项工作非常有意义，因为发现这些偏微分方程通常非常困难，因为它提供了一种方法来加速计算杠杆的应用。

这为生成类似OEIS(整数序列在线百科全书)的资源提供了机会。这允许任何领域的研究和搜索这些数据库，看看类似的问题是否已经解决，或者相关的序列或结构是否已经存在，而不需要重新开始。

02 迅速「入门」

在PDE有守恒量的情况下，它们可以积累(例如，能量是质量弹簧的守恒量)。

所以，研究人员可以将OptPDE设计成一个两部分的系统，——

(1)计算任何PDE的守恒量（CQ）数量；

找出使n_CQ最大化的偏微分方程。

下面是(1)在一些熟悉的系统中的实际应用。

因为研究人员寻找n_CQ的方法是可以微分的，所以只需要在PDE中训练项指数，通过SGD最大化n_CQ，就可以找到新的微分方程。

他们以u__为由x => u_xxx^三是以项目为基础，运行5000次。

下面是3D解决方案 PCA——

研究人员发现，他们得到的大部分解决方案都是四个偏微分方程家族的线性组合，其中一个是KdV方程的一种形式，另外三个方程完全是新的，没有记录在文献中！

因此，研究人员决定，在这些新的可积偏微分方程中，至少有一个守恒量。

也就是说，在AI的帮助下，人类科学家发现了一些全新的可积偏微分方程！

然而，要解释和分析这些发现，仍然要依靠人类科学家。

研究人员仔细分析了下列简化版的红色偏微分方程。（u_t=u_x^发现它表现出断裂、无限的CQ，而幂律衰减为三角波。

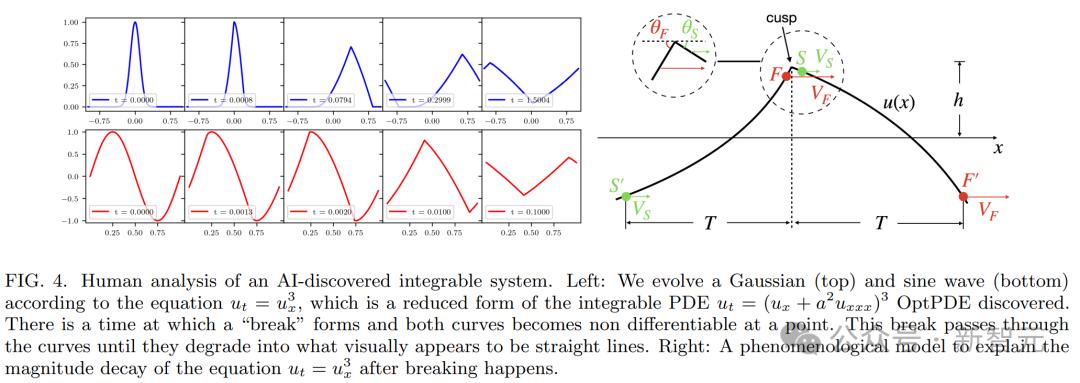
此后，科学家们很有希望利用OptPDE来发现更多新颖的可积偏微分方程，从而模拟物理上的复杂现象。

然而，OptPDE要求人工智能与人类科学家协调工作。作者呼吁，如果这种模式能够被物理学界接受，科学家很可能会在使用现代人工智能工具之前做出更多的新发现。

03 可积系统：极为罕见，难以发现。

由于易于处理、可预测、可控，可积系统在物理和工程系统中发挥着重要作用。

但是，它们极为罕见，难以发现。

在传统中，发现可积系统的方法是依靠纸笔，它强调符号推送，并考虑可能的系统和守恒量。（CQ）指数级大搜索空间，效率极低。

因此，MIT科学家认为：AI能做些什么？

所以，他们引入了OptPDE的可积系统发现解决方案。

以前很多工作都是利用极端的学习从物理数据和微分方程中发现守恒量的，但是MIT研究者的方法是微分方程最可以解释的。

此外，以前的方法不能积极优化和设计偏微分方程。

不过，这个AI可以做到！

尽管过去机器学习方法已被用来发现守恒量，但这项工作首次提出——

AI和人类科学家可以通过验证和解释集成系统来协调工作。

04 论文方法

研究者通过下列阶段来构建这种方法。

1.CQFinder——寻找PDE的守恒量。

2.OptPDE——在CQFinder中使用

，找出可积PDE。

图1反映了整个过程。但需要注意的是，这个过程需要人类科学家输入CQ和PDE基础，与人工智能协调，这就需要了解这一领域的知识。

OptPDE的可视化管道。为PDE提供基础，OptPDE将提高指数，从而最大限度地提高PDE的守恒量(CQ) 数量。起初，u会衰减，不守恒，但OptPDE会通过将扩散项归零来发现更守恒的指数。这个可视化的例子很简单，但是由于PDE基础广泛，OptPDE可以帮助人类科学家发现新颖的可积系统。

为构建OptPDE，必须首先设计CQFinder，以准确计算任何PDE的CQ。

具体而言，一阶偏微分方程需要一个有空间变量X的时间，其形式是

。

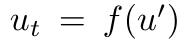
其中，

它是u及其空间导数的集合，并且具有自由初始条件。

。

研究人员应考虑形式。

的守恒量。

对CQ量而言，它必须在u的整个时间演变中保持恒定。

CQ的时间不变性可以表示为：

其中，

。

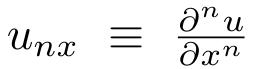
尽管这个方程看起来很复杂，但是只需要考虑一个简单的设置，其中h，(u′) 它是k个预定义基函数的线性组合，

。

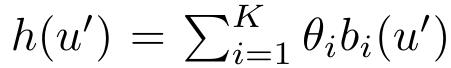
这里，研究人员需要处理两个无限大的问题。

1. 从理论上讲，对于任何光滑的u，都必须建立线性方程；在实践中，可以测试方程是否可以与这个无限函数集相似。

2. 理论上，积分是存在的(-∞,∞)在实践中，需要使用有限的范围来类似于它(在范围之外将u强制为零)。

研究人员希望在CQFinder中建立子流程，然后进行简单的稀疏化和识别解决方案，因为它很容易被人类科学家解释。

具体而言，研究人员需要将PDE参数化为预定PDE的线性组合，

。

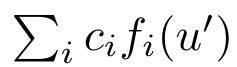
采用固定PDE，CQFinder输出其守恒总数。

由于CQFinder是由PyTorch编写的，因此它原则上是可以微分的，因此，研究人员可以通过自动微分来识别PDE指数中的哪些扰动会增加CQ。

但是，可微性最大的挑战是守恒量本质上是分散的(例如，偏微分方程可以有3或4个守恒量，而不是3.7个)。

为反向传播提升指数提升指数。

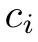
， 目标函数

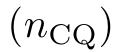
必须是可以忽略的。

针对这一情况，研究人员引入了sigmoid函数。

平滑版本。

04 论文结果

CQFinder基准测试

为验证CQFinder是否能像每个人想象的那样工作，研究人员在Burgers、Korteweg-DeVries(Kd)与薛定谔方程三个测试系统一起运行。

图2显示，奇异值曲线显示从小到大的快速变化，然后可以清楚地区分消失值和非消失值。

这样就证明了CQFinder不仅能够正确计算守恒总数，而且还能够得到它们的符号公式。

AI发现了三个新颖的可积系统。

研究人员发现，全新的可积系统可以通过使用Opt-PDE最大化守恒量来定位OptPDE的流形。

一般选用PDE作为单个方程。

，其中

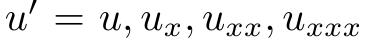
，P是多项式最多3次。

实际上，研究人员使用广义球坐标，自然强制归一化指数。

研究人员在OptPDE中使用A=0，B=1000，epochs=25000，学习率为10^-3，余弦退火，Tmax=5000。

研究人员运行OptPDE，随机抽取其它33个参数的5000个初始位置。

随后，研究人员使用3D 对OptPDE结果进行PCA可视化返回参数值分析，如图3所示。

可以看出，解的流形结构很有意思：两边有两个极点，环形解位于中间。

2个极点代表

，这种方法可以积累KdV方程，而环形的解更加复杂。

研究人员对这些环形的解中进行了插值。

接着，他们找到了三个偏微分方程组作为环形子空间的基础，如图3所示。

守恒量表明，这三个偏微分方程中的每一个都是新的，而且本质上是有趣的。(如附录I所示)

研究人员将重点放在以下偏微分方程上，因为它的方法非常紧凑——

在这个方程的a=1前提下，研究人员运行了CQFinder，发现它有一个非凡的CQ。——

研究人员通过一系列冗长的代数操作，验证了数值和符号，

确实是

的CQ。

在这里，研究人员可以肯定：OptPDE发现了一个新的偏微分方程家族，他们承认有趣的守恒能力。——

。

人的责任：解释AI的发现

而且在这里，MIT的研究人员表示，下一步人类将承担起责任！

人类科学家应该做的，是利用AI找到的偏微分方程家族，并进行解释。

文章中，研究者仅限于分析a。≪一种情况，促进

这一特殊情况代表了一个真正的可积系统，并且有无限数量的CQ。也就是

所有的n都是守恒的。

研究人员在Mathematica中绘制了具有高斯和正弦初始条件的偏微分方程的演变，如图所示。

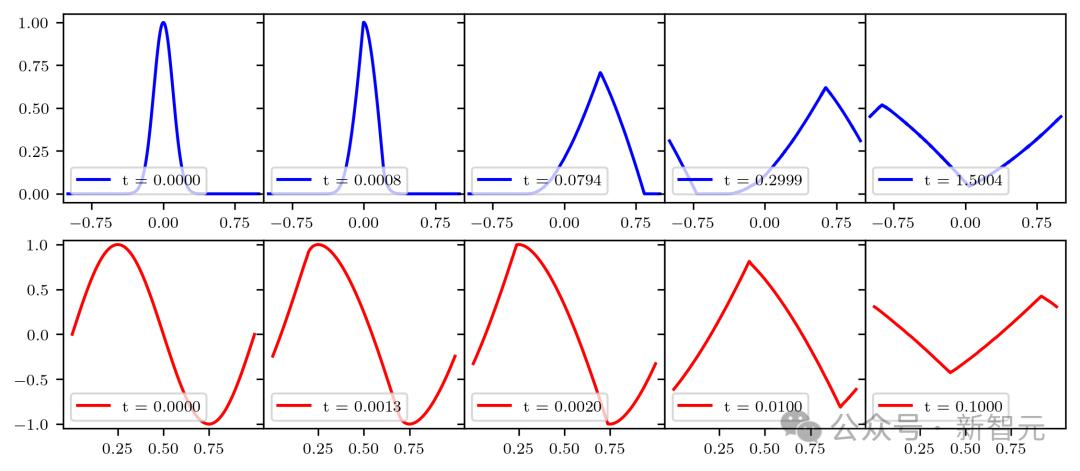
从视觉上看，演变似乎是一种波，在break 在time之后，它已经衰退为一种线性重量，此时，波在某一点上变得不可微分。

研究人员推导了break time的符号模式，并且是breakk中的方程式 time之后的行为，创造了一个现象学模型。

Break Time

研究人员注意到，通过在x的两侧进行积分，可以使公式4与Burgers公式相似。

利用特征方程，可以跟踪稳定u的路径，找出两个特征相交的最早时间。

最终可以得出，Break Time为

，在附录L中，这与研究人员的模拟结果大致一致。

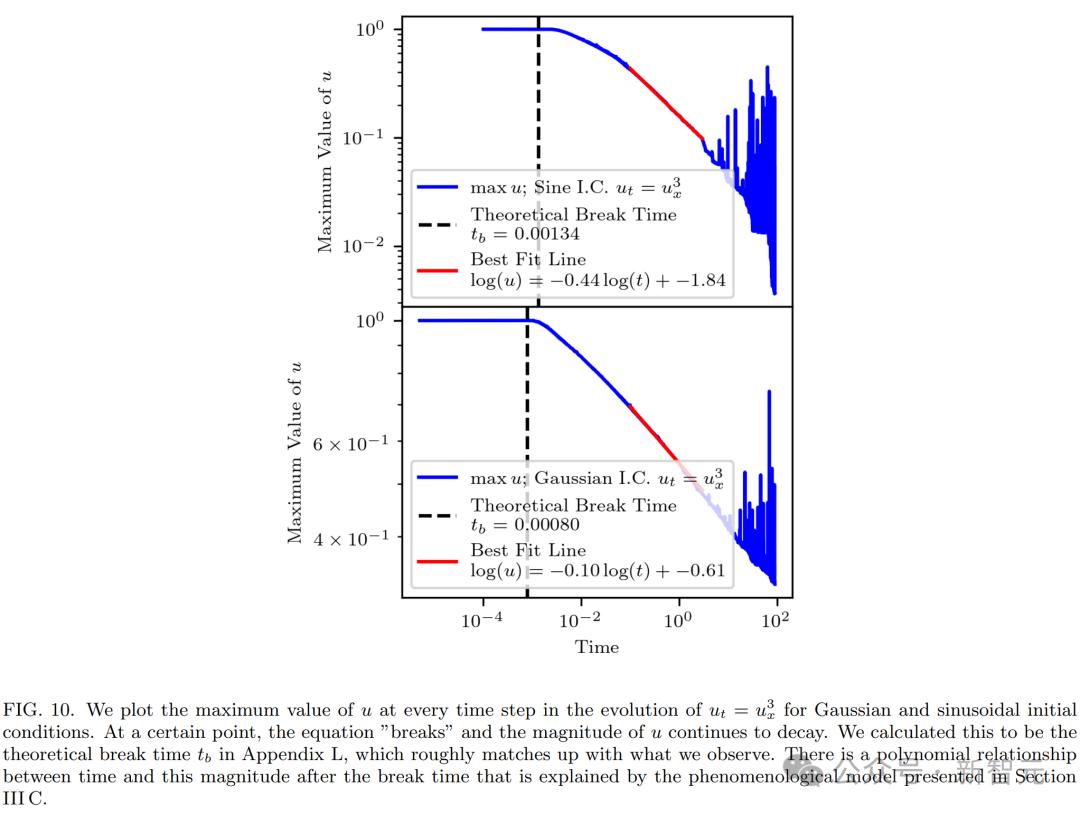
现象学模型

为了理解波break之后的行为，研究人员希望建立一个现象模型来解释波接近三角波时的动态。

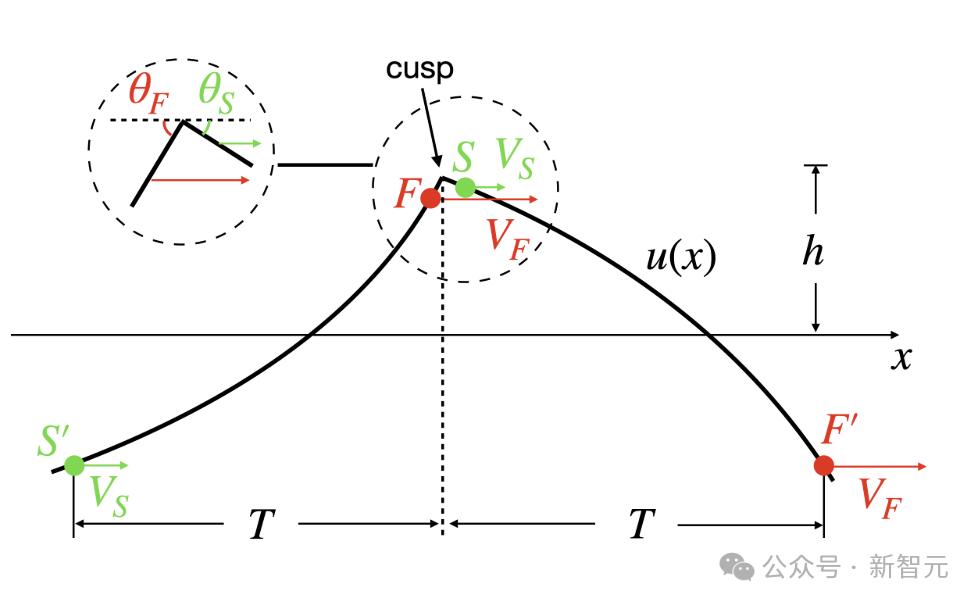
对于这一点，研究人员进行了如下推导。

其中一种特殊情况就是a=1，当曲线沿高度匀称收缩时，就会得到。

，这种情况符合正弦波的情况。

理解其它解决方案

从图3可以看出，研究者得到的解是高级和非线性的，其立方项由三阶导数组成。

利用物理的直觉来处理这些问题可能是令人望而生畏的，但是研究人员注意到，三阶导数正在出现。 在KdV方程中，或者，如果推导出具有稳定性和其他阻力的弦的波动方程，也会出现三阶导数。

物理学中很少见到非线性多项式方程，但是它确实存在，比如高速运动时的空气阻力公式。

。

所以，在物理变化建模中，复杂的微分方程是很有用的。

对于其它结果，研究人员表示，希望其他科学家也能参与其中，共同解释。

总而言之，这种人类科学家与人工智能合作的范式，是由MIT研究者引入的，极有可能鼓励人类科学家为物理学做出新的发现！

本文来自微信微信官方账号“新智元”（ID:AI_era），作者：新智元，36氪经授权发布。

本文仅代表作者观点，版权归原创者所有，如需转载请在文中注明来源及作者名字。

免责声明：本文系转载编辑文章，仅作分享之用。如分享内容、图片侵犯到您的版权或非授权发布，请及时与我们联系进行审核处理或删除，您可以发送材料至邮箱：service@tojoy.com